데이터가 많이 있을때 이 중 약간의 샘플을 추출하여 그 샘플의 성격을 평가하는 일은 이바닥(?)에서 종종 있는 일입니다. 다들 층화추출(유사한 성격의 데이터를 그룹지어놓고, 각 그룹에서 랜덤으로 샘플을 뽑는 방식으로 전체 데이터의 샘플을 구하면 좋은 샘플이 나온다)는 많이 들어보셨을테니, 여기서는 그 외의 기법들에 대해 적어보겠습니다.

* 비 추정(ratio estimation)
예를들어, 한국 전체 가정의 평균 외식비를 알고 싶다고 합시다. 그리고 다음과 같이 일정한 확률로 랜덤하게 샘플을 추출해서 6개의 샘플을 얻었습니다.

20
40
61
79
102
119

그러면 모집단(한국 전체 가정)에 대한 평균 외식비를 우리는 (20+40+61+79+102+119)/6=70.16667로 계산할 수 있습니다. 여기까지가 단순 임의 추출법(simple random sampling)에 의한 방법입니다.

하지만 만약 외식비와 상관관계가 높은 각 가정의 월급을 알고 있다면 ratio estimation을 사용할 수 있습니다. 예를들어 다음의 데이터가 있다고 해보겠습니다.

월급	외식비
10	20
20	40
30	61
40	79
50	102
60	119

그리고 한국의 모든 가정의 평균 월급이 35만원이라는 것을 이미 알고 있다고 해보겠습니다. 그러면 다음과 같이 외식비를 추정할 수 있습니다.

35 * (20+40+61+79+102+119)/(10+20+30+40+50+60)= 35 * 210 / 421 = 70.45843.

이 값은 앞서서 구한 70.16667과 비교할때 약간의 차이가 있습니다.

70.16667이나 70.45843이나 둘다 모평균(한국 가정의 평균 외식비)에 대한 비편향(기대값이 모수와 같음) 추정량입니다. 하지만 이 둘의 분산은 다릅니다. 즉, 예~전에 배운 통계학 지식을 떠올려보면 모수를 추정할 때, 95%의 신뢰도로 70.45843 플러스 마이너스 얼마와 같이 구간으로 추정한다는 것이 생각날 것입니다. 바로 그 플러스 마이너스 되는 값이 작다는 이야기입니다.

이처럼 한가지 값 Y를 추정할 때, 그와 상관계수가 0.5 이상이 되는 X를 알고 있고 Y와 X를 선형 회귀하였을때 y축 절편이 0을 지나면 항상 ratio estimation이 simple random sampling보다 정확도가 높게 됩니다.

y축 절편이 0을 지난다는 말은 값들이 이렇게 생겼단 말입니다.

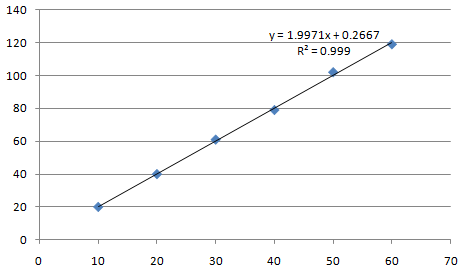
그림에서 상관계수는 sqrt(R^2)=sqrt(0.9999)가 됩니다.

* 회귀 추정

그러나 앞서와 달리 y와 x가 원점을 지나지 않게 선형 관계를 가지고 있다면 비추정은 할 수 없습니다. 예를들어서, 월급과 외식비가 다음과 같았다고 해보겠습니다.

월급	외식비
10	30
20	50
30	71
40	89
50	112
60	129

이 값들을 선형회귀하면 다음과 같습니다. (이 그림은 엑셀에서 분산형 그래프를 그린다음에 점에다가 마우스 오른쪽 버튼 클릭하고 추세선추가 하면 자동으로 나옵니다. 뭔가 특별한 소프트웨어가 필요 없습니다.)

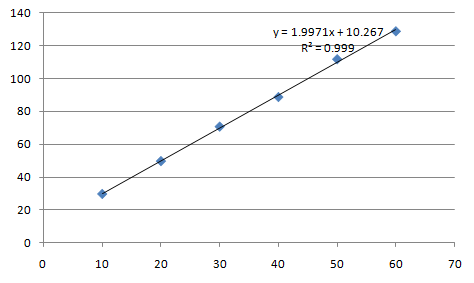
이 경우는 y절편이 10.267로 큽니다. 그러면 회귀식

\hat{\mu_y}= \overline{y} + b(\mu_x - \overline{x})

를 이용하여 외식비의 모평균을 추정합니다.

여기서

\hat{\mu_y}

가 모수(한국 각 가정 외식비 평균)에 대한 추정치이고,

\overline{x}

가 샘플로 얻은 월급의 평균,

\overline{y}

는 샘플로 얻은 외식비 평균,

\mu_x

는 한국 전체 가정의 월급의 평균입니다. 샘플 월급의 평균이나 샘플 외식비 평균은 주어진 것이니 쉽게 알 수 있고, 한국 전체 가정의 월급의 평균은 사전에 알고 있어야 합니다.

b

는 회귀분석하는 방법으로 풀면 됩니다.

b = \dfrac{\Sigma(x_i - \overline{x})(y_i - \overline{y})}{\Sigma(x_i - \overline{x})^2}

즉 비추정이나 회귀추정이나, 이렇게 이미 알고 있는 x라는 녀석으로 y를 잘 알아내보자 이런것이죠.

회귀를 사용한 추정은 회귀를 사용하지않은 simple random sampling에 비해 항상 분산이 작아 항상 더 정확합니다. 당연하게도 특히 상관계수의 절대값이 1에 가까울수록 분산이 작아집니다.

* 계통 추출법(systematic sampling)

계통 추출법이 가장 놀라운 내용중 하나인데요. 가장 간단하게 샘플을 구하면서 오히려 simple random sampling보다 정확도가 높은 방법입니다. 예를들어, 다음과 같은 외식비가 있을때

20, 32, 11, 102, 57, 35, 99, 78, 9, 85

simple random sampling은 이걸 하나하나 보면서 얘를 뽑을까 말까 결정하면서 샘플을 뽑습니다. 예를들어 5개의 샘플을 구하겠다고 하면 저 위의 숫자가 10개이므로 50% 확률로 각 수를 뽑는 것이죠.

예를들자면 이렇게 뽑히겠죠.

20, 32, 102, 99, 9

한편 계통추출법은 일정 간격으로 샘플을 뽑는 방법입니다. 이를 가장 효과적으로 적용하려면 먼저 이 숫자들을 sort해야합니다.

9, 11, 20, 32, 35, 57, 78, 85, 99, 102

그 다음, 10개중 5개를 뽑을거니까 추출간격은 10/5=2가 됩니다. 제일 처음할일은 첫번째 숫자를 뽑는것인데 추출간격이 2니까 1과 2중에 숫자를 하나 정합니다. 예를들어 1을 뽑았다고 하면, 샘플로 첫번째 숫자인 9를 얻게됩니다. 그 다음부터는 기계적으로 2씩 간격을 두고 뽑습니다. 그러면 샘플은 이렇게 됩니다.

9, 20, 35, 78, 99

간단하죠?

간단한데다가 놀라운 점은 이렇게 sort를 하고 샘플을 뽑으면 그 분산이 simple random sampling의 분산보다 작아진다는 것입니다. 즉 95% 신뢰도로 플러스 마이너스 얼마얼마나 하는 그 얼마얼마 부분의 값이 작아져 더 정확하다는 말입니다.

이 예에서는 그런일이 없었지만, 동일간격으로 샘플을 뽑다보면 n개 샘플을 원했지만 n+1개 샘플이 뽑힐 수도 있습니다. 하지만 샘플의 크기 n이 충분히 크다면 한두개 많고 적은건 문제가 없습니다.

그리고 당연하겠지만 데이터를 소팅 안하고 뽑으면 simple random sampling과 다를 바가 없게 됩니다. 하지만 데이터에 사이클이 있을 경우 (즉, 운나쁘게도 간격 2마다 동일한 성격의 데이터가 온다면) 최악의 상황이 나타납니다.

예를들어 데이터가

9, 102, 11, 99, 32, 85, 35, 78, 57

라면 샘플은

9, 11, 32, 35, 57

이 되고 이 샘플은 명백히 bias가 있습니다.

따라서 소트하기 싫으면 최소한 사이클이 없는지 보고 나서 적용해야하고, 최상은 값을 미리 소트하는 것입니다. 아니면 데이터가 어찌하다보니 미리 소트되어있다면 적용 안할 이유가 없는 기법인 것이죠.