Let’s build artificial data:
> x = 1:100 > y = 3*x + rnorm(100, 0, 0.1)
Now, y has 3*x + error (which follows independent normal distribution.)
> y [1] 3.084463 5.921660 9.043298 11.863854 14.975701 17.980051 20.812897 23.950546 27.013619 29.879748 33.029797 [12] 35.933785 39.032856 42.021709 45.150473 47.988470 51.005696 53.921992 56.956936 60.154561 62.870397 66.056555 [23] 68.818562 71.878614 75.037485 77.971538 81.212420 84.075885 86.924858 89.879004 92.987709 96.250259 98.866730 [34] 101.816094 104.976485 108.138008 111.180993 114.016497 117.019846 119.892135 123.005147 125.958263 129.165459 131.892357 [45] 134.985222 137.992608 141.158806 144.089719 146.924594 149.944683 153.130148 156.113614 158.992470 162.068371 165.093236 [56] 168.134131 171.038950 174.138382 176.801168 180.132722 183.137894 185.884679 188.922193 192.098572 195.171722 198.037255 [67] 201.071104 204.023956 206.970078 209.960827 212.839931 215.842587 218.939796 221.790648 225.065676 228.100543 231.090998 [78] 233.996619 236.942362 239.952409 242.805987 246.144036 248.835554 251.792460 255.217650 257.822964 260.989347 264.009189 [89] 267.065940 270.070240 272.876032 275.924888 279.106800 282.153525 284.942045 288.031658 290.881470 293.930968 296.895243 [100] 299.968869
Build a model:
> m = lm(y ~ x) > m Call: lm(formula = y ~ x) Coefficients: (Intercept) x -1.168e-05 3.000e+00
This shows that yhat = 3.0 * x – 1.168e-05. Let’s check the goodness of this model:
> summary(m)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.204330 -0.074342 -0.004509 0.079480 0.252437
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.168e-05 2.239e-02 -0.001 1
x 3.000e+00 3.849e-04 7793.923 —
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1111 on 98 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 6.075e+07 on 1 and 98 DF, p-value: < 2.2e-16
Adjusted R-squared says that 100% of variation is explained by this linear regression, and we can see that t value of x has p < 0.05 meaning that x is statistically meaningful in this model. It’s easy to draw some diagrams:
> par(mfrow=c(2,2)) > plot(m)
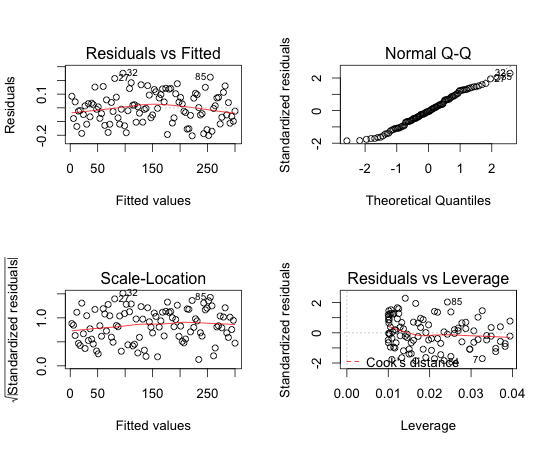
Residual VS Fitted looks fine (though it would have been much nicer if the line were totally flat). Normal Q-Q plot shows us that residual follows a normal distribution.
Let’s make an intentional mistake. In the following we will try to model y = ax + bz + c while y is actually 3x + error:
> z = runif(100, 0, 50)
> m2 = lm (y ~ x + z)
> m2
Call:
lm(formula = y ~ x + z)
Coefficients:
(Intercept) x z
0.0052540 2.9999384 -0.0002374
> summary(m2)
Call:
lm(formula = y ~ x + z)
Residuals:
Min 1Q Median 3Q Max
-0.199865 -0.075759 -0.007949 0.077534 0.256803
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0052540 0.0284124 0.185 0.854
x 2.9999384 0.0003872 7747.345 z -0.0002374 0.0007824 -0.303 0.762
—
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1116 on 97 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 3.009e+07 on 2 and 97 DF, p-value: < 2.2e-16
As one can see, z’s p value is 0.762 which is larger than 0.05 meaning that the value is not useful in modeling. Let’s compare m and m2 using ANOVA:
> anova(m, m2)
Analysis of Variance Table
Model 1: y ~ x
Model 2: y ~ x + z
Res.Df RSS Df Sum of Sq F Pr(>F)
1 98 1.2098
2 97 1.2087 1 0.0011466 0.092 0.7623
This shows that the model 2 is not too different from model 1 (as p value 0.7623 is larger than 0.05, they’re not statistically different model.) Therefore, it’s fine to think that z is meaningless. (Recall that p value of z shows that z is not meaningful.)
We may find y ~ x starting from y ~ x + z automatically:
> step(m2, scope=list(lower=y ~ 1, direction=”backward”))
Start: AIC=-435.57
y ~ x + z
Df Sum of Sq RSS AIC
- z 1 0 1 -437.47
1 -435.57
- x 1 747884 747885 895.98
Step: AIC=-437.47
y ~ x
Df Sum of Sq RSS AIC
1 -437.47
- x 1 749891 749892 894.25
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-1.168e-05 3.000e+00
Final model from step was y ~ x. When we removed z, AIC became -437.47 while AIC of y ~ x + z was -435.57 (smaller AIC is better).
Let’s perform boxcox transformation. For that, let’s change x to sqrt(x):
> x = 1:100
> y = 3 * x + rnorm(100, 0, 0.1)
> x = sqrt(x)
> m3 = lm(y ~ x)
> summary(m3)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-17.535 -14.181 -4.509 11.042 60.449
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -93.8145 5.1147 -18.34 x 36.5330 0.7197 50.76 —
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 16.75 on 98 degrees of freedom
Multiple R-squared: 0.9634, Adjusted R-squared: 0.963
F-statistic: 2576 on 1 and 98 DF, p-value: < 2.2e-16
This model looks good, but boxcox transformation may make it better:
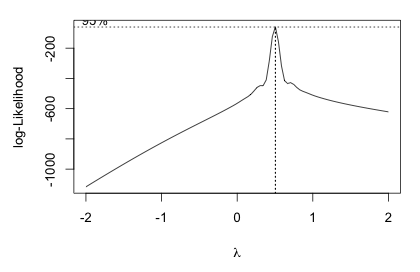
> library(MASS) > boxcox(m3) > bc = boxcox(m3)
> bc$x[which.max(bc$y)] [1] 0.5050505
bc$x and bc$y are points in the above plot. Thus, we can see that lambda = 0.5050505 has max. likelihood. To apply that:
> m4 = lm(I(y^0.5050505) ~ x)
> summary(m4)
Call:
lm(formula = I(y^0.5050505) ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.020409 -0.008784 -0.001066 0.006676 0.091507
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0916328 0.0044541 -20.57 x 1.7903556 0.0006268 2856.43 —
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01458 on 98 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 8.159e+06 on 1 and 98 DF, p-value: < 2.2e-16
Now we have much better Adjusted R-square. Or we may do forward-backward selection:
> m5 = lm(y ~ 1)
> step(m5, list(lower=y~1, upper=y~x+z), direction=”both”)
Start: AIC=894.27
y ~ 1
Df Sum of Sq RSS AIC
+ x 1 722550 27484 565.62
750034 894.27
+ z 1 2015 748019 896.00
Step: AIC=565.62
y ~ x
Df Sum of Sq RSS AIC
27484 565.62
+ z 1 45 27439 567.46
- x 1 722550 750034 894.27
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
-93.81 36.53
But this is not a silver bullet; it’s better to find better feature in the first place.
References)
1. R Cookbook by Paul Teetor. Copyright 2011 Paul Teetor, 978-0-596-80915-7.
2. 구자용, 박현진, 최대우, 김성수, 데이터마이닝, KNOU Press.