앞서 포스팅한 Quiz: NxN matrix의 좌하단에서 우상단으로 가는 방법의 수의 첫번째 솔루션입니다. 이 방법은 완벽한 정답을 구하는 것은 아니고, Monte Carlo Method를 통해 근사치만 구합니다. 물론 Knuth가 Selected Papers on Computer Science에서 설명한 방법입니다.

다음과 같이 3×3 matrix가 있다고 하겠습니다.

이때, 최초 출발점 좌하단에서 임의의 방향으로 한 칸 이동합니다. 최초 이동 가능 방향은 U(위), R(우측) 뿐입니다. 따라서 다음 그림과 같이 R로 이동할 확률은 1/2 입니다.

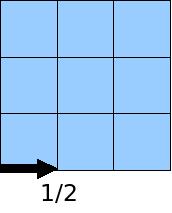
그 자리에서 다시 이동하려고 하면 한번 방문한 점은 재방문이 불가능하므로 R과 U만 선택가능합니다. 이때 U를 택했다면 이러한 이동이 택해질 확률은 1/2입니다.

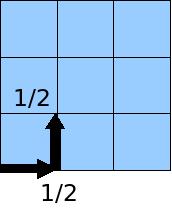
이번에는 L(좌측), U, R 중 하나의 방향으로 이동할 수 있습니다. 따라서 R로 이동할 경우 이러한 이동이 택해질 확률은 1/3입니다.

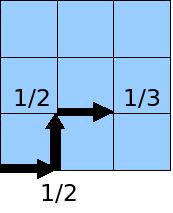
이런 방식으로 매 위치마다 하나의 방향을 택하면서 가면서, 최종적으로 우상단 점에 도달하는 path를 구합니다. 또 이 path가 나타날 확률을 각 위치에서 특정 이동을 택할 확률의 곱으로서 구합니다. 위 그림의 예에서는 (1/2) * (1/2) * (1/3) * … 이 그 확률이 되겠죠. 그리고 나면, 하나의 path와 그 path 가 나타날 확률을 얻게됩니다.

아시다시피 그 확률의 역수를 구하면 경우의 수가 됩니다. 그래서 만약 어떤 path가 구해질 확률이 1/12342로 나왔다면, 전체 path의 개수는 12342임을 알 수 있습니다. 물론 특정 path 는 다른 path보다 더 많이 나타날 수 있으며, 이 문제는 간단하게는 위 시행을 여러번 반복해서 평균을내어 전체 path의 개수를 구하는 것으로 해결할 수 있습니다. 보다 정밀하게 error를 bound하는 풀이가 가능할 수도 있겠지만, 정확하게 정답을 구하는 방법이 또 별도로 존재하니 삽질이겠죠..